增长量计算很复杂?学会这一招就够了!
在你学习资料分析的道路上,是否见过类似这样的列式呢?
这样的呢?
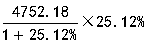
这样的呢?
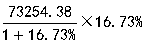
……
我相信,你一定遇到过!即使之前你没遇见,在后面的学习过程中,你也一定会遇上的!
它们,有一个共同的特点—都是增长量的求解列式。
在资料分析的学习中,增长量问题是始终绕不过去的知识点,这是一个几乎逢考必考的考点。而最常见的增长量出题模式,就是已知现期量和增长率,求解增长量,此时就要用到“增长量= ”这个公式(其中,A表示现期量,r表示增长率),是不是跟上面的三个式子长得很像呢?
”这个公式(其中,A表示现期量,r表示增长率),是不是跟上面的三个式子长得很像呢?
由于增长量这个考点很常规、很基础,所以对于同学们来讲,判断考点和列式,通常都不是问题,问题在于如何快速计算。那么接下来,我们就好好聊聊这个问题怎么算。
在学完本文之后,我希望你再次遇到增长量问题时,脑海里应该立马蹦出一个方法—特征分数法。
在“增长量=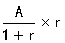 ”这个公式,增长率r通常是一个百分数(如25.12%、33.43%...),如果用百分数进行计算就比较麻烦。如果可以将增长率这个百分数转化成一个分数(
”这个公式,增长率r通常是一个百分数(如25.12%、33.43%...),如果用百分数进行计算就比较麻烦。如果可以将增长率这个百分数转化成一个分数(![]() ),此时,原式就可做如下化简:
),此时,原式就可做如下化简:
①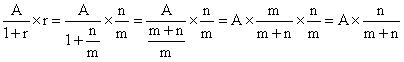
当然,增长率也可能是一个负数,此时
②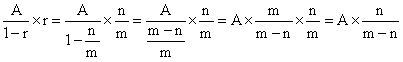
神马,你管这个叫化简?这看着也不简单啊,那我们来看两个例题吧,你就知道为啥要这样做了。
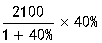
【解析】40%=![]() ,原式=
,原式=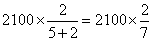 =600。
=600。
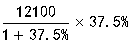
【解析】37.5%=![]() ,原式=
,原式=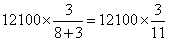 =3300。
=3300。
是否,有感觉到这个算法的妙处了呢?
事实上,r=![]() 还并不是用的最多的,用的更多(同时也更简便)的是r=
还并不是用的最多的,用的更多(同时也更简便)的是r=![]() 的时候,此时
的时候,此时
③
当增长率为负数时
④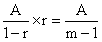
注:③④式(r=![]() )的推导过程,就只是把①②式(r=
)的推导过程,就只是把①②式(r=![]() )中的n全部换成1即可。
)中的n全部换成1即可。
对于③④式的用法,我们也来看几个例题(尝试口算!!!):
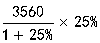
【解析】因为25%=![]() ,原式=
,原式=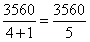 =712。
=712。
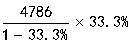
【解析】因为33.3%≈![]() ,原式≈
,原式≈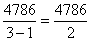 =2393。
=2393。
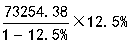
【解析】因为12.5%=![]() ,原式=
,原式=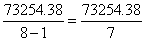 ≈10500。
≈10500。
相信这些例题,你通过口算,是完全可以解决的吧!
你也应该能够感受到,特征分数法求解增长量是非常好用的吧!
但是,好用归好用,如果对于特征分数不熟悉,好用的方法也仅仅只是摆设!
比如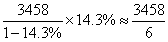 ≈576(因为14.3%≈
≈576(因为14.3%≈![]() ),此时你如果不知道14.3%≈
),此时你如果不知道14.3%≈![]() 的话,原式的化简也就无从谈起。
的话,原式的化简也就无从谈起。
所以,常用的百分数与分数的转化关系,你就必须、必须、必须把它背下来,没有任何商量的余地!
常用的特征分数对照表如下:
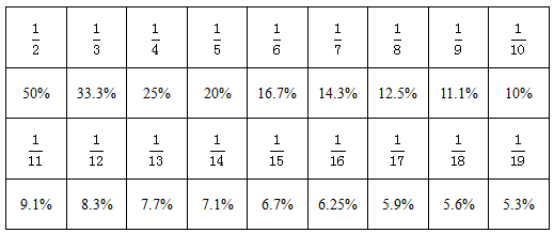
熟记上述数据之后,我们再来练习几个试题:
【例1】2009年俄罗斯是世界最大的管道天然气出口国,占管道天然气总出口量的27.8%,出口量为1764.8亿立方米,较2008年增长14.3%。
问题:2009年俄罗斯管道天然气出口较上年增长了多少亿立方米( )?
A.110 B.221 C.332 D.443
【解析】一般增长量计算。
由材料可知:2009年俄罗斯管道天然气出口量为1764.8亿立方米,较2008年增长14.3%。则所求增长量=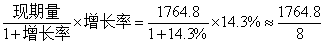 ≈221亿立方米。故本题答案为B项。
≈221亿立方米。故本题答案为B项。
【例2】2019年,全年全国居民人均可支配收入30733元,比上年增长8.9%。按常住地分,城镇居民人均可支配收入42359元,比上年增长7.9%。城镇居民人均可支配收入中位数39244元,比上年增长7.8%。农村居民人均可支配收入16021元,比上年增长9.6%,扣除价格因素,实际比上年增长6.2%。农村居民人均可支配收入中位数14389元,比上年增长10.1%。全国农民工人均月收入3962元,比上年增长6.5%。
问题:2019年,全国农村居民人均可支配收入中位数比上年增加约( ) 元。
A.1230 B.1320 C.1380 D.1403
【解析】一般增长量计算。
由材料可知:2019年全国农村居民人均可支配收入中位数14389元,比上年增长10.1%。则所求增长量=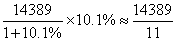 ≈1308元,接近B选项。故本题答案为B项。
≈1308元,接近B选项。故本题答案为B项。
以上,是特征分数法对增长量问题的求解。而这,仅仅是特征分数法的用途之一。关于特征分数法,还有很多巧妙的用途,我们会在后续的文章中,给大家一一道来,敬请期待……
原标题:增长量计算很复杂?学会这一招就够了!
来源:金标尺教育
 地区
地区 考试科目
考试科目 抖音
抖音 023-67417095
023-67417095


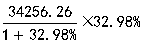




 点击下载
点击下载





